State Estimation Using Kalman Filter
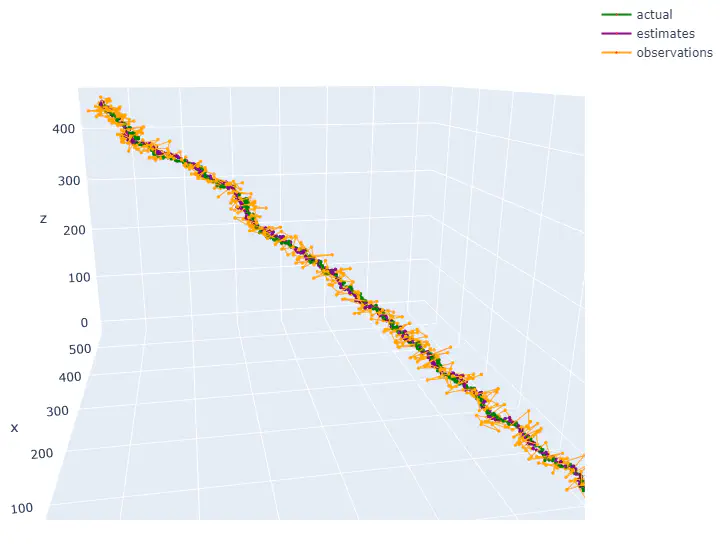Plots of actual, observed and estimated trajectory- Consider an airplane flying in a 3D world. A noisy sensor (e.g., GPS positions) provides measurements $z_t = [x'_t, y'_t, z'_t]$. The plane is controlled by providing velocity increments $u_t = [\delta \dot{x}_t, \delta \dot{y}_t, \delta \dot{z}_t]$, which get added to the velocity components $\dot{x}_t$, $\dot{y}_t$ and $\dot{z}_t$ at each time step. The uncertainty in the motions is characterized by a presence of Gaussian noise $\epsilon_t \sim \mathcal{N}(0, R)$. Similarly, the measurement uncertainty is characterized by presence of Gaussian noise $\delta_t \sim \mathcal{N}(0, Q)$. The goal is to estimate its positions $[x_t, y_t, z_t]$ and velocities $[\dot{x}_t, \dot{y}_t, \dot{z}_t]$ at time instant $t$ from noisy observations $[x’_t, y’_t, z’_t]$
- The problem setup is extended by incorporating an additional observation. Assume that there are certain landmarks (e.g., air traffic control towers) at the following known locations in the environment: $(150, 0, 100)$, $(-150, 0, 100)$, $(0, 150, 100)$, and $(0, -150, 100)$. The aircraft can measure the Euclidean distance (range) to a landmark when its true position within a certain range of the landmark and the measurement is corrupted with Gaussian noise $\eta_t \sim \mathcal{N}(0, S)$. At any instant, the agent receives a single measurement from the nearest landmark and the measurement can be uniquely associated with the corresponding landmark. Note that the landmark-distance observation is in addition to the GPS-positions that the agent is receiving
Shubh Goel
Computer Science
My research interests include Embodied AI, Computer Vision and Deep Learning.